Centripetal force of an object in an arbitrary curve

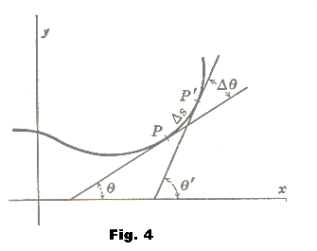
Let's assume that an object moves in an arbitrary curve which is described by y=y(x). We want to find the centripetal force that acts on the object in any point. 

Well, we know that the centripetal force for an object moving in a circle is mυ^2/R, where R is the radius of the circle, m the mass and υ the velocity. 

If we assume that any point of the arbitrary curve is also a point of  hypothetical circle of radius R(x), then finding the function R(x) means that we can calculate the centripetal force (mυ^2/R(x)) at any point. 

Let's take a small part of the curve with length dS. As a part of circle with radius R(x) it has a length of dS=R.dθ. As a part of the curve y(x) it has a length of sqrt(1+y'^2)dx, where y'=dy/dx. That is, 

R. dθ=sqrt(1+y'^2)dx, or,  R.θ' = sqrt(1+y'^2), where θ'=dθ/dx.

We know that tanθ=dy/dx=y'. Differentiating we get, θ' = cos^2(θ).y'' But we know that cos^2(θ)(1+y'2)=1. 

So we finally get that: R(x) = (1+y'2)^(3/2) / y''.

Source of image: SolitaryRoad